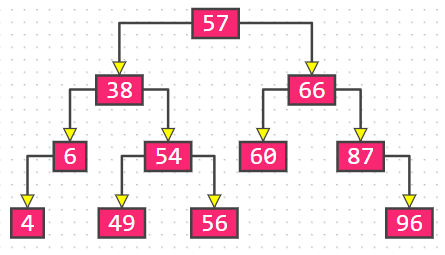
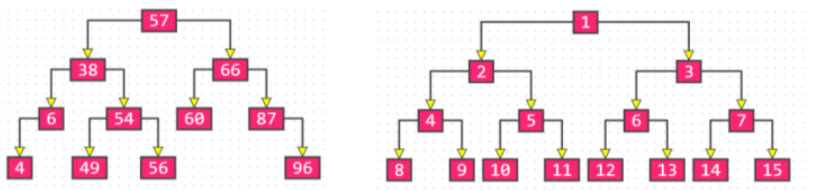
二叉树(BinaryTree)

◼ 二叉树的特点

每个节点的度最大为 2（最多拥有 2 棵子树）
左子树和右子树是有顺序的

即使某节点只有一棵子树，也要区分左右子树

◼ 二叉树是有序树还是无序树？

有序树

二叉树的性质：

非空二叉树的第i层，最多有2^i-1个节点（i≥1)
在高度为h的二叉树上最多有2h-1个结点（h≥1)
对于任何一棵非空二叉树，如果叶子节点个数为n0，度为2的节点个数为n2，则有: n0= n2+1

假设度为1的节点个数为n1，那么二叉树的节点总数n = n0 + n1 + n2

二叉树的边数T =n1+ 2*n2 = n- 1 = n0 + n1 + n2-1

因此n0 = n2+ 1

边的计算：

从结点度数看：结点度数就是边数

从结点看：每个节点顶部都有一条边，整棵树除了根节点都有一条边

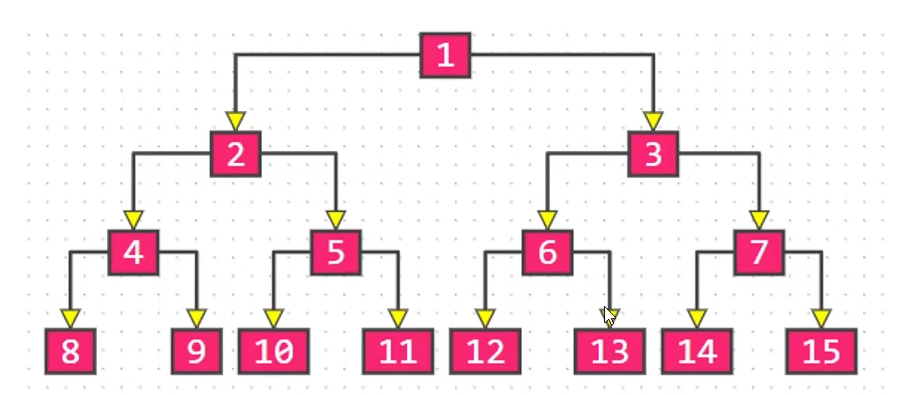
真二叉树(Proper Binary Tree)

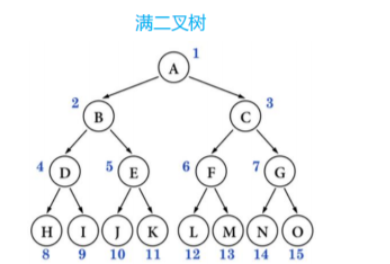
满二叉树(Full Binary Tree)

满二叉树:所有节点的度都要么为0，要么为2。且所有的叶子节点都在
最后一层

在同样高度的二叉树中，满二叉树的叶子节点数量最多、总节点数量最多
满二叉树一定是真二叉树，真二叉树不一定是满二叉树

假设满二叉树的高度为h (h≥ 1)，那么

第i层的节点数量:2^(i-1)

叶子节点数量: 2^(h-1)

总节点数量n

n= 2^h -1 = 2^0+2^1＋2^2＋…+ 2^(h-1)

h = log2(n+ 1)

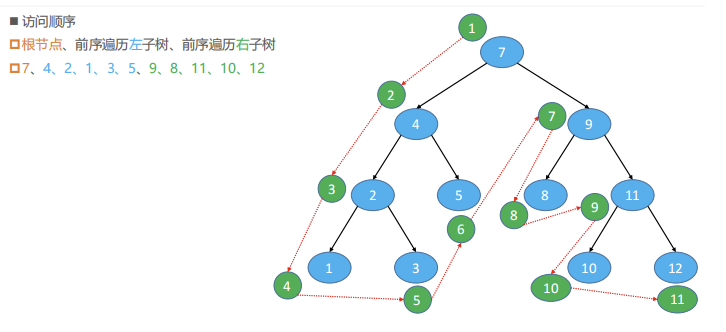
二叉树的遍历：

前序遍历（Preorder Traversal）

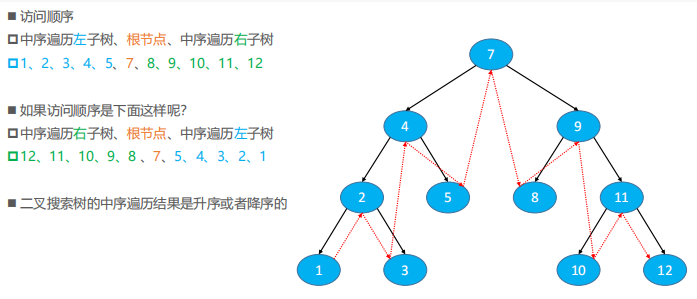
中序遍历（Inorder Traversal）

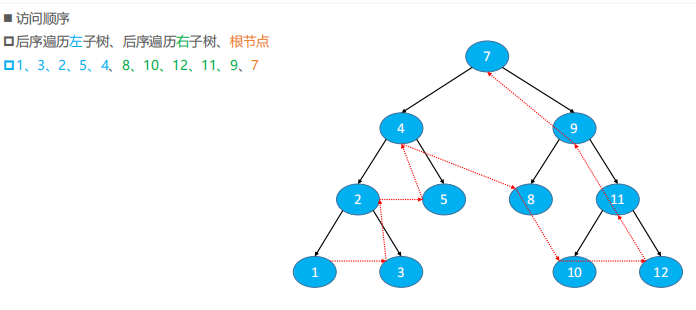
后序遍历（Postorder Traversal）

层序遍历（Level Order Traversal）

前序遍历：

递归实现：

public class BinaryTreePreorderTraversal {


    /**
     * 先序遍历递归
     * @param root
     * @return
     */
    public List<Integer> preorderTraversal(TreeNode root) {
        List<Integer> list = new LinkedList<>();
        traverse(root, list);
        return list;
    }

    private void traverse(TreeNode root, List<Integer> list) {
        if (root == null) {
            return;
        }
//        首先将根节点放入数组中
        list.add(root.val);
//        遍历左节点
        traverse(root.left, list);
//        遍历右子节点
        traverse(root.right, list);

    }

    public static void main(String[] args) {
        BinaryTreePreorderTraversal binaryTreePreorderTraversal = new BinaryTreePreorderTraversal();
        TreeNode newNodeA = new TreeNode(1);
        TreeNode newNodeB = new TreeNode(2);
        TreeNode newNodeC = new TreeNode(3);
        newNodeA.right = newNodeB;
        newNodeA.left = null;
        newNodeB.left = newNodeC;
        newNodeB.right = null;
        newNodeC.right = null;
        newNodeC.left = null;
        binaryTreePreorderTraversal.preorderTraversal(newNodeA).stream().forEach(e->{

            System.out.print(e+",");

        });


    }
}

中序遍历（Inorder Traversal）

递归实现：

    private void traverse(TreeNode root, List<Integer> list) {
        if (root == null) {
            return;
        }

//        遍历左节点
        traverse(root.left, list);
        //
        list.add(root.val);
//        遍历右子节点
        traverse(root.right, list);
    }

栈实现：

//    使用栈进行遍历
    /**
     * 循环结束条件：结点不为空,且入栈不为空
     * 首先进行遍历至树的根节点，加入栈中，然后依次出栈，并判断右子树是否为空，不为空以同样的方式进行
     * 遍历
     */

    public  List<Integer> inorderTraversalByStack(TreeNode root){
        List<Integer> list = new ArrayList<>();
     
        ;
        while (root!=null||! stk.isEmpty()){
            while (root!=null){
                stk.push(root);
                root=root.left;
            }
            root = stk.pop();
            list.add(root.val);
            root=root.right;

        }
        return list;
    }

后序遍历（Postorder Traversal）

public List<Integer> postorderTraversal(TreeNode root) {
      LinkedList<Integer> res = new LinkedList();
      traverse(root, res);
      return res;
  }

  /**
   * 先遍历左子树在遍历右子树
   *
   * @param root
   * @param res
   */
  public void traverse(TreeNode root, List<Integer> res) {

      if (root == null) {
          return;
      }
      traverse(root.left, res);
      traverse(root.right, res);
      res.add(root.val);
  }

栈实现：

    /**
     * 从根节点遍历至左节点，加入栈中，如果最后一个为空，加入，如果弹出结点含有右子节点那抹将当前结点装入并重新
     * 开始遍历
     *首先找到左节点，依次入栈
     * 
     * @return
     */
    public List<Integer> postorderTraversalByStack(TreeNode root) {
        LinkedList<Integer> res = new LinkedList();
        if (root == null) {
            return res;
        }

        TreeNode prev = null;
        Deque<TreeNode> stack = new LinkedList();
        while (root != null || !stack.isEmpty()) {
//          从左节点开始进行遍历
            while (root != null) {
                stack.push(root);
                root = root.left;
            }
            root = stack.pop();
//            需要找到根节点，
            if (root.right == null || root.right == prev) {
//                记录写入的结点值，当访问的是同一个值时结束遍历
                res.add(root.val);
                prev = root;
                root = null;
            } else {
//                根节点会被访问两次
                stack.push(root);
//                如果有右节点，替换右节点
                root = root.right;
            }
        }
        return res;
    }

层序遍历：

@author
  * @date: 2022/3/6
  */
//    两个循环，第一重是树的下一层元素,第二是将该层遍历完全
    public List<List<Integer>> levelOrder(TreeNode root) {
     List<List<Integer>> list = new ArrayList<>();
        Deque<TreeNode> que = new LinkedList();
        que.addLast(root);
        List<Integer> eachLayer ;

            if (root==null){
                return Collections.emptyList();
            }

        while (!que.isEmpty()){
//            获取单前层的长度
            int count = que.size();
            eachLayer = new ArrayList<>();
            while ( count>0){
                TreeNode first = que.pop();
                eachLayer.add(first.val);
                if (first.left!=null){
                    que.addLast(first.left);
                }
                if (first.right!=null){
                    que.addLast(first.right);
                }
//                当前层遍历完进去下一层
                    count--;
            }
            list.add(eachLayer);
        }
        return  list;
    }

}

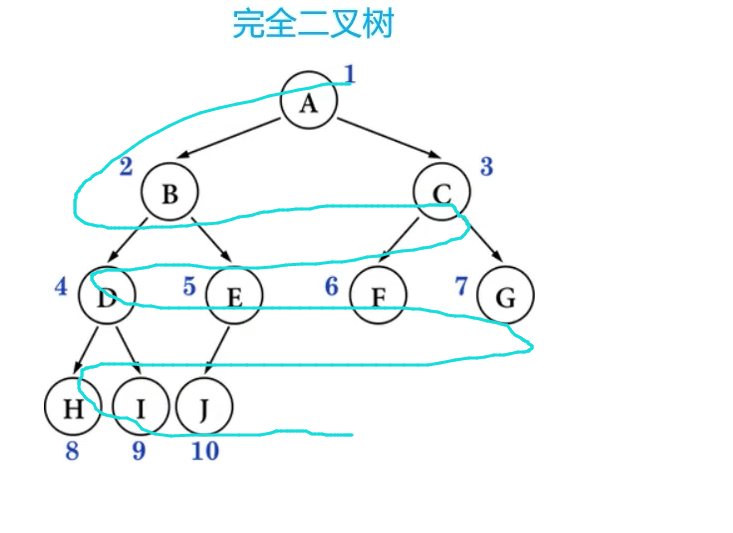
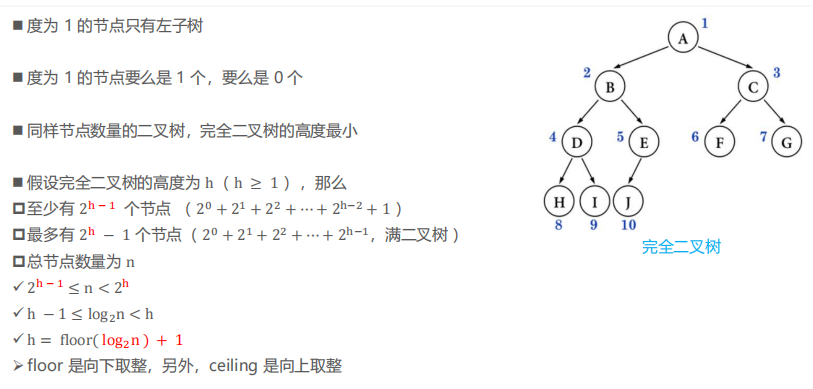
完全二叉树(Complete Binary Tree)

完全二叉树:叶子节点只会出现最后2层，且最后1层的叶子结点都靠左对齐

从上到下，从左到右依次排列

叶子节点只会出现最后2层，最后1层的叶子结点都靠左对齐
完全二叉树从根结点至倒数第⒉层是一棵满二叉树
满二叉树一定是完全二叉树，完全二叉树不一定是满二叉树

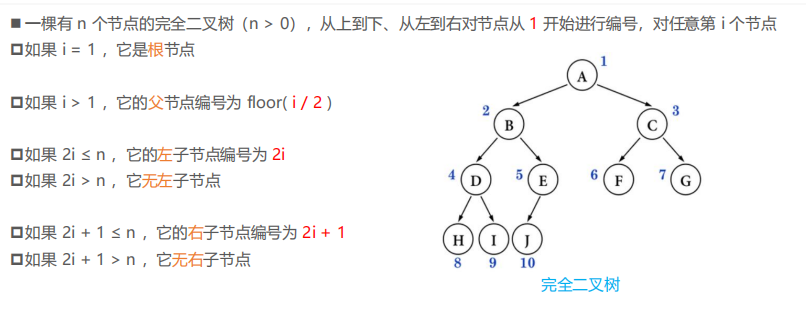
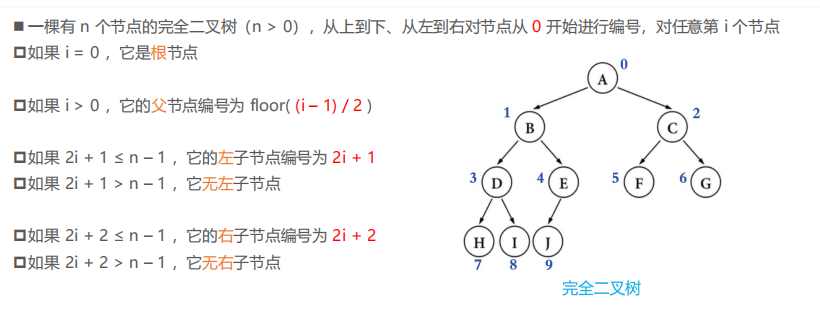
完全二叉树性质：

面试题

1
2
3

        System.out.println(5/2);//2
//        向下取整
        System.out.println(5>>2);/1

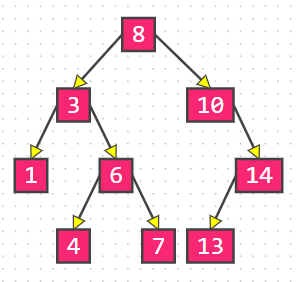
二叉搜索树(Binary Search Tree):

◼ 在 n 个动态的整数中搜索某个整数？（查看其是否存在）

◼ 假设使用动态数组存放元素，从第 0 个位置开始遍历搜索，平均时间复杂度：O(n)

◼ 如果维护一个有序的动态数组，使用二分搜索，最坏时间复杂度：O(logn)

但是添加、删除的平均时间复杂度是 O(n)

◼ 针对这个需求，有没有更好的方案？

使用二叉搜索树，添加、删除、搜索的最坏时间复杂度均可优化至：O(logn)

◼ 二叉搜索树是二叉树的一种，是应用非常广泛的一种二叉树，英文简称为 BST

又被称为：二叉查找树、二叉排序树

任意一个节点的值都大于其左子树所有节点的值

任意一个节点的值都小于其右子树所有节点的值

它的左右子树也是一棵二叉搜索树

◼ 二叉搜索树可以大大提高搜索数据的效率

◼ 二叉搜索树存储的元素必须具备可比较性

比如 int、double 等

如果是自定义类型，需要指定比较方式

不允许为 null

接口设计

◼ int size() // 元素的数量

◼ boolean isEmpty() // 是否为空

◼ void clear() // 清空所有元素

◼ void add(E element) // 添加元素

◼ void remove(E element) // 删除元素

◼ boolean contains(E element) // 是否包含某元素

删除结点：

度为2的结点：

先从前驱或者后继节点的值覆盖原结点的值