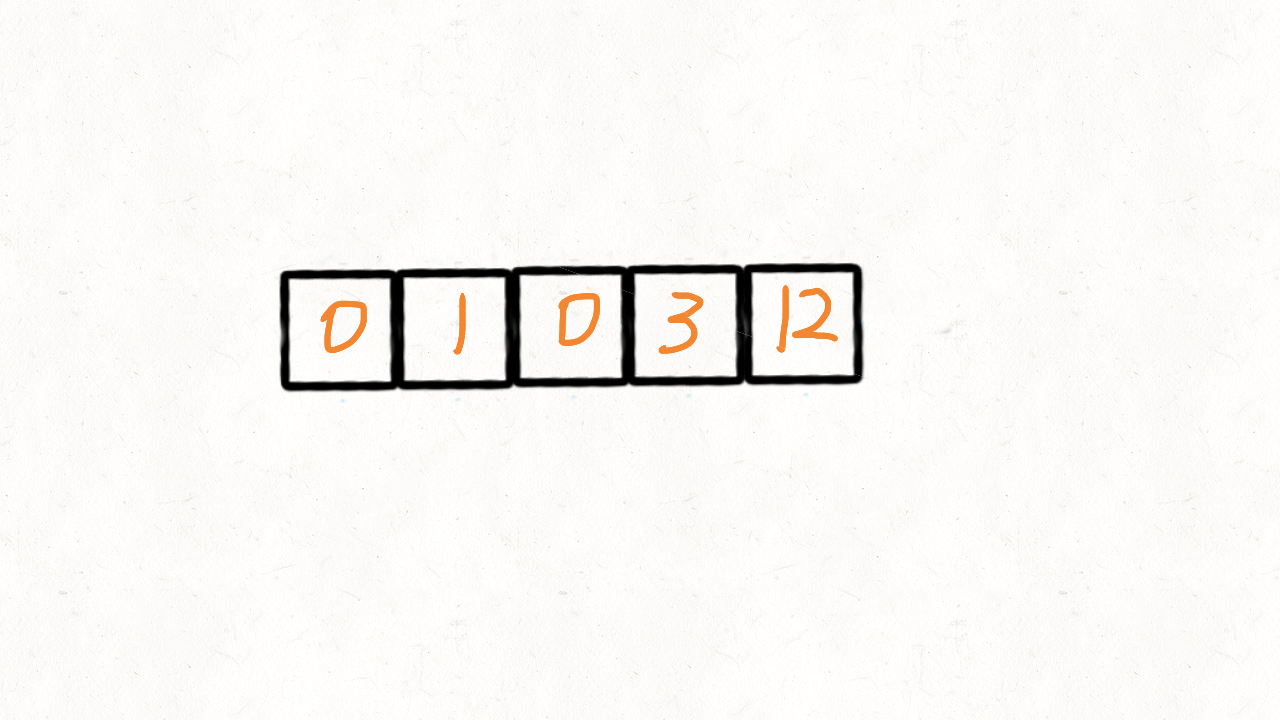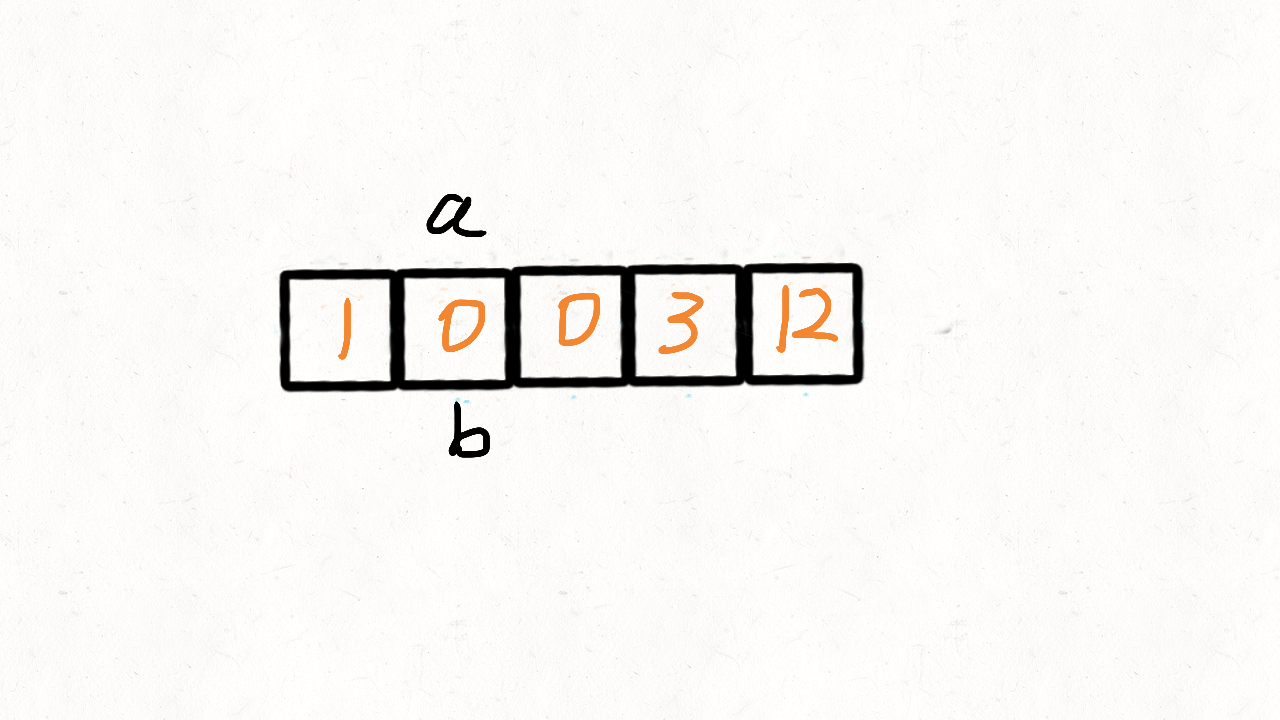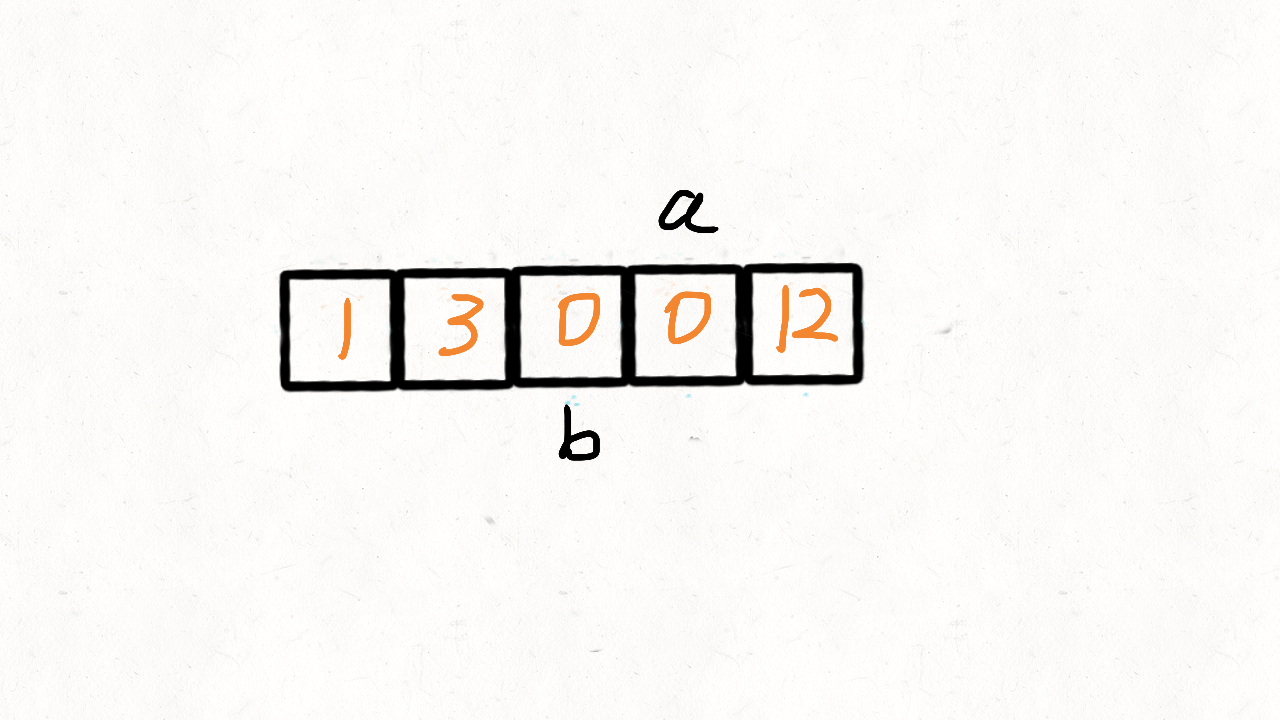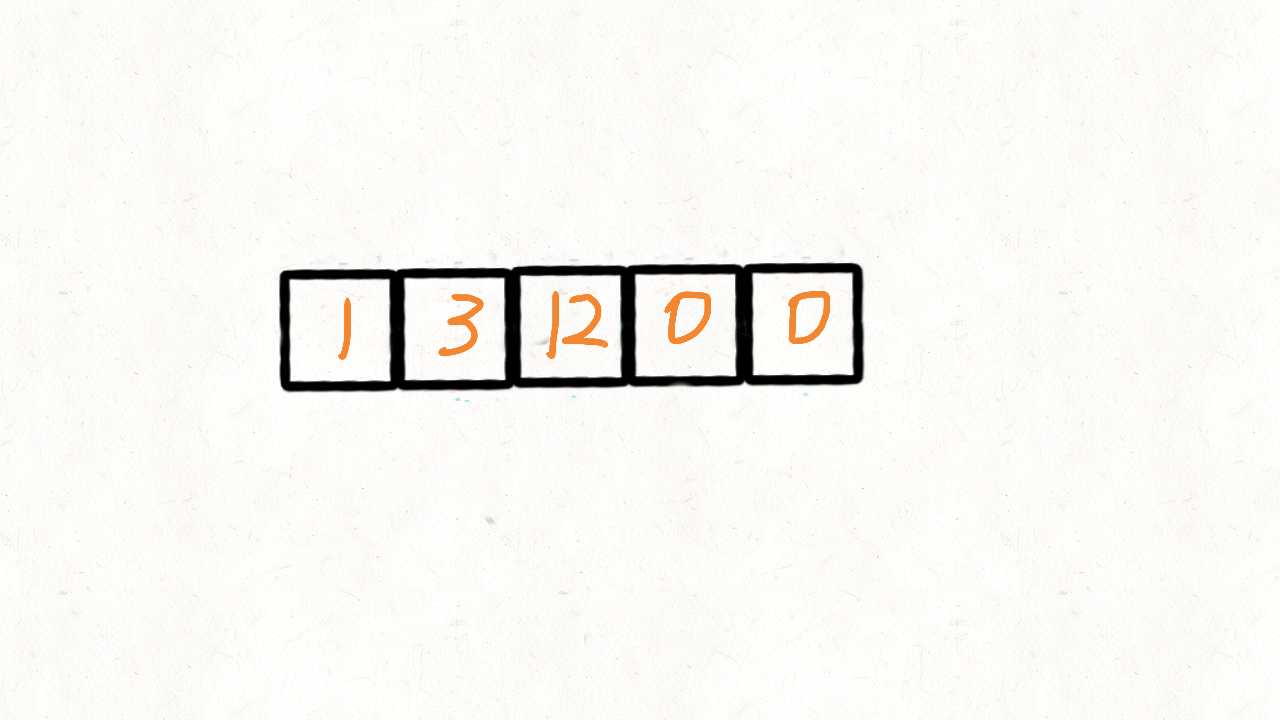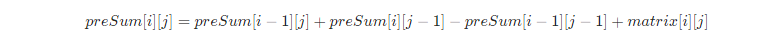数组：

移动零（双指针）

动画演示 283.移动零 - 移动零 - 力扣（LeetCode） (leetcode-cn.com)

给定一个数组 nums，编写一个函数将所有 0 移动到数组的末尾，同时保持非零元素的相对顺序。

示例 1:

1
2
输入: nums = [0,1,0,3,12]
输出: [1,3,12,0,0]

首先要确定一个待分割的元素做中间点x，然后把所有小于等于x的元素放到x的左边，大于x的元素放到其右边。
这里我们可以用0当做这个中间点，把不等于0(注意题目没说不能有负数)的放到中间点的左边，等于0的放到其右边。
这的中间点就是0本身，所以实现起来比快速排序简单很多，我们使用两个指针i和j，只要nums[i]!=0，我们就交换nums[i]和nums[j]一次进行遍历：

  • 时间复杂度: O(n)
  • 空间复杂度: O(1)

283_2.gif

没有优化之前：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
    /**
     * @description: 使用先后指针，前指针进行遍历,当前指针遇见不等于零时，与最后一个指针元素进行交换，最后一个
     * @author jwz
     * @date: 2022/2/28
     */
    public int[] moveZero(int[] nums) {

//         当前指针指向的值不为0时，就和末尾的指针进行交换,同时末尾指针加一
//        结束  条件 ：末尾等于length-1
        for (int i = 0, j = 0; i < nums.length - 1; ) {
            i++;
            //        必须是前指针不为0，后指针为0的才可以交换
            if (nums[i] != 0 && nums[j] == 0) {
                int temp = nums[i];
                nums[i] = nums[j];
                nums[j] = temp;
                j++;
                /*前指针为0 后指针不为0的情况，不进行交换且后指针往前移动*/
                //        int[] z = {1,0,1};
            } else if (nums[i] == 0 && nums[j] != 0) {
                j++;
                //   前指针不为0，后指针也不为0的情况。后指针往前移动
                //        int[] z = {4,2,4,0,0,3,0,5,1,0};
            } else if (nums[i] != 0 && nums[j] != 0) {
                j++;
            }
        }
        return nums;
    }

优化之后

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
    public int[] moveZero01(int[] nums) {
        int length;
        if (nums == null || (length = nums.length) == 0) {
            return nums;
        }
        int j = 0;
        for (int i = 0; i <=length-1; i++) {

            if (nums[i] != 0) {
//                但只有一个元素时候 不能够进行交换[1]
                if (i>j){
//                    直接将元素进行赋值
                    nums[j] = nums[i];
                    nums[i] = 0;
                }
                j++;
            }
        }
        return nums;
    }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

    public static void main(String[] args) {
        MoveZeroes283 moveZeroes283 = new MoveZeroes283();

        int[] z = {0, 1, 0, 3, 12};
//        必须是前指针不为0，后指针为0的才可以交换
//        int[] z = {2,1};
        //          前指针为0  后指针不为0的情况
//        int[] z = {1,0,1};
//        前指针和后指针都不为0的情况
//        int[] z = {4,2,4,0,0,3,0,5,1,0};
        Arrays.stream(moveZeroes283.moveZero01(z)).forEach(
                e -> {
                    System.out.println(e + ",");
                }
        );

    }

区域和检索 - 数组不可变（前缀和）

image-20220417163214829

image-20220417163244307

普通解法：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class NumArray {

    private int[] nums;

    public NumArray(int[] nums) {
        this.nums = nums;
    }
    
    public int sumRange(int left, int right) {
        int res = 0;
        for (int i = left; i <= right; i++) {
            res += nums[i];
        }
        return res;
    }
}

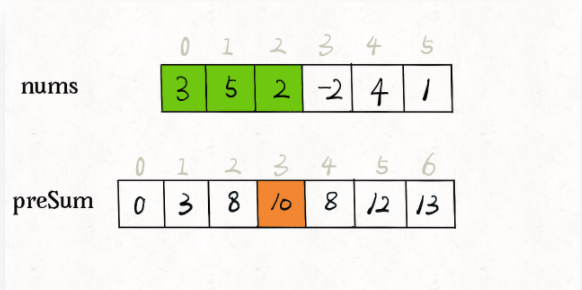
image-20220326205502741

看这个 preSum 数组，如果我想求索引区间 [1, 4] 内的所有元素之和，就可以通过 preSum[5] - preSum[1] 得出。

这样，sumRange 函数仅仅需要做一次减法运算，避免了每次进行 for 循环调用，最坏时间复杂度为常数 O(1)。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
  
private int preNums[];
   
public NumArray(int[] nums) {
    //  两两相加数组长度比原来的要大
  preNums = new int[nums.length+1];
    preNums[0] =0;
    //不能写等于原因，preNum数组比nums长1，会数组下标越界
   for(int i =1;i<preNums.length;i++){
        preNums[i] = preNums[i-1]+ nums[i-1];
   }    

}
 // 计算 nums 的累加和
public int sumRange(int left, int right) {
      /* 查询闭区间 [left, right] 的累加和 */
   int res = preNums[right+1]-preNums[left];
      
   return res;
}

应用场景

比方说，你们班上有若干同学，每个同学有一个期末考试的成绩（满分 100 分），那么请你实现一个 API，输入任意一个分数段，返回有多少同学的成绩在这个分数段内。

那么，你可以先通过计数排序的方式计算每个分数具体有多少个同学，然后利用前缀和技巧来实现分数段查询的那么，你可以先通过计数排序的方式计算每个分数具体有多少个同学，然后利用前缀和技巧来实现分数段查询的 API：

1
2
3
4
5
6
7
8
9
10
11
int[] scores; // 存储着所有同学的分数
// 试卷满分 100 分
int[] count = new int[100 + 1]
// 记录每个分数有几个同学
for (int score : scores)
    count[score]++
// 构造前缀和
for (int i = 1; i < count.length; i++)
    count[i] = count[i] + count[i-1];

// 利用 count 这个前缀和数组进行分数段查询

二维矩阵中的前缀和

https://leetcode-cn.com/problems/range-sum-query-2d-immutable

image-20220417163438912

image-20220417163458450

步骤一：求 preSum
我们先从如何求出二维空间的 preSum[i][j]。

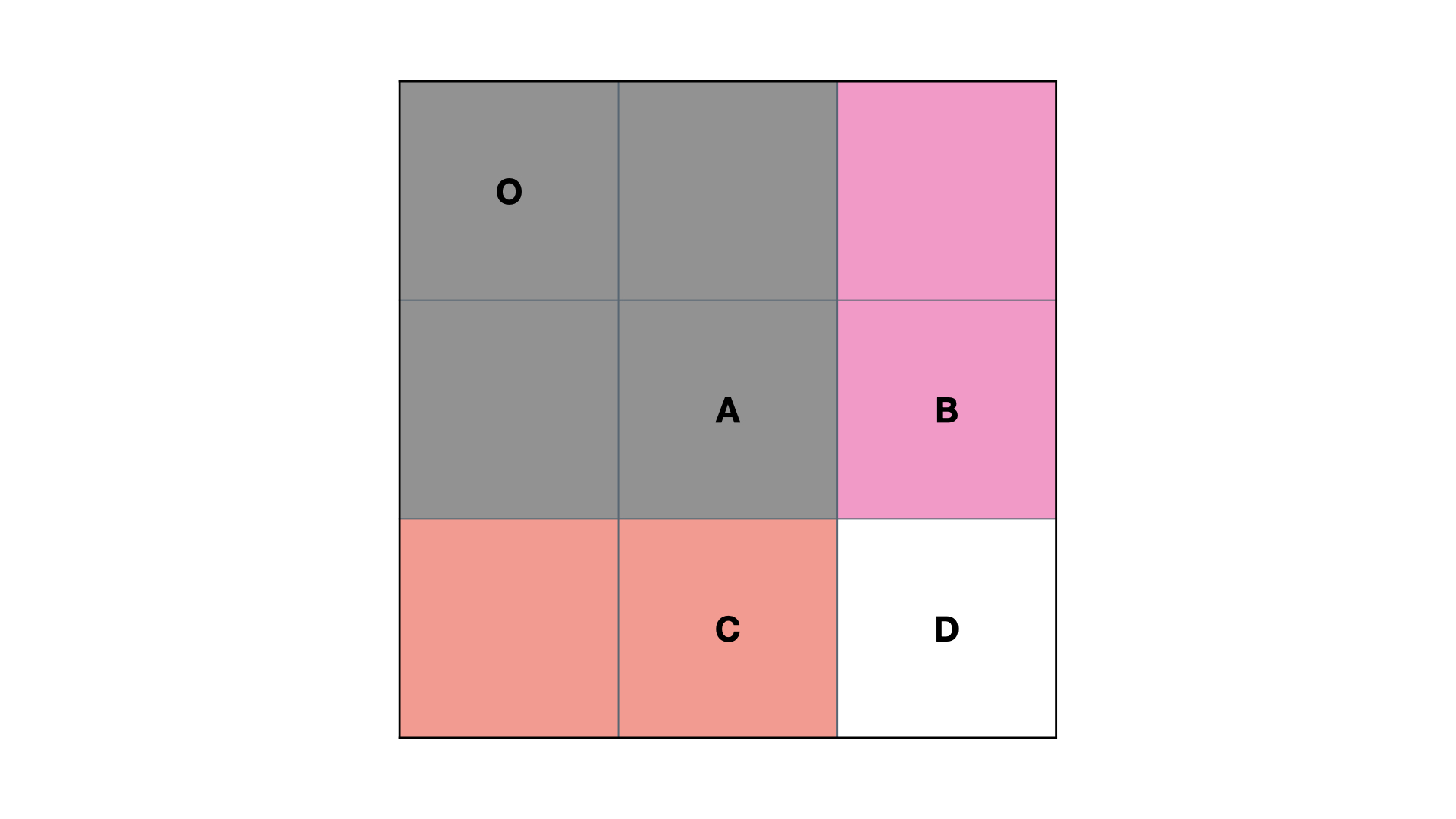
我们定义 preSum[i][j]preSum[i][j] 表示 从 [0,0][0,0] 位置到 [i,j][i,j] 位置的子矩形所有元素之和。
可以用下图帮助理解：

S(O, D) = S(O, C) + S(O, B) - S(O, A) + D

304.001.jpeg

减去 S(O, A)S(O,A) 的原因是 S(O, C)S(O,C) 和 S(O, B)S(O,B) 中都有 S(O, A)S(O,A)，即加了两次 S(O, A)S(O,A)，所以需要减去一次 S(O, A)S(O,A)。

如果求 preSum[i][j]表示的话，对应了以下的递推公式：

image-20220327105618467

根据 preSum 求子矩形面积：

前面已经求出了数组中从 [0,0][0,0] 位置到 [i,j][i,j] 位置的 preSum。下面要利用 preSum[i][j]preSum[i][j] 来快速求出任意子矩形的面积。

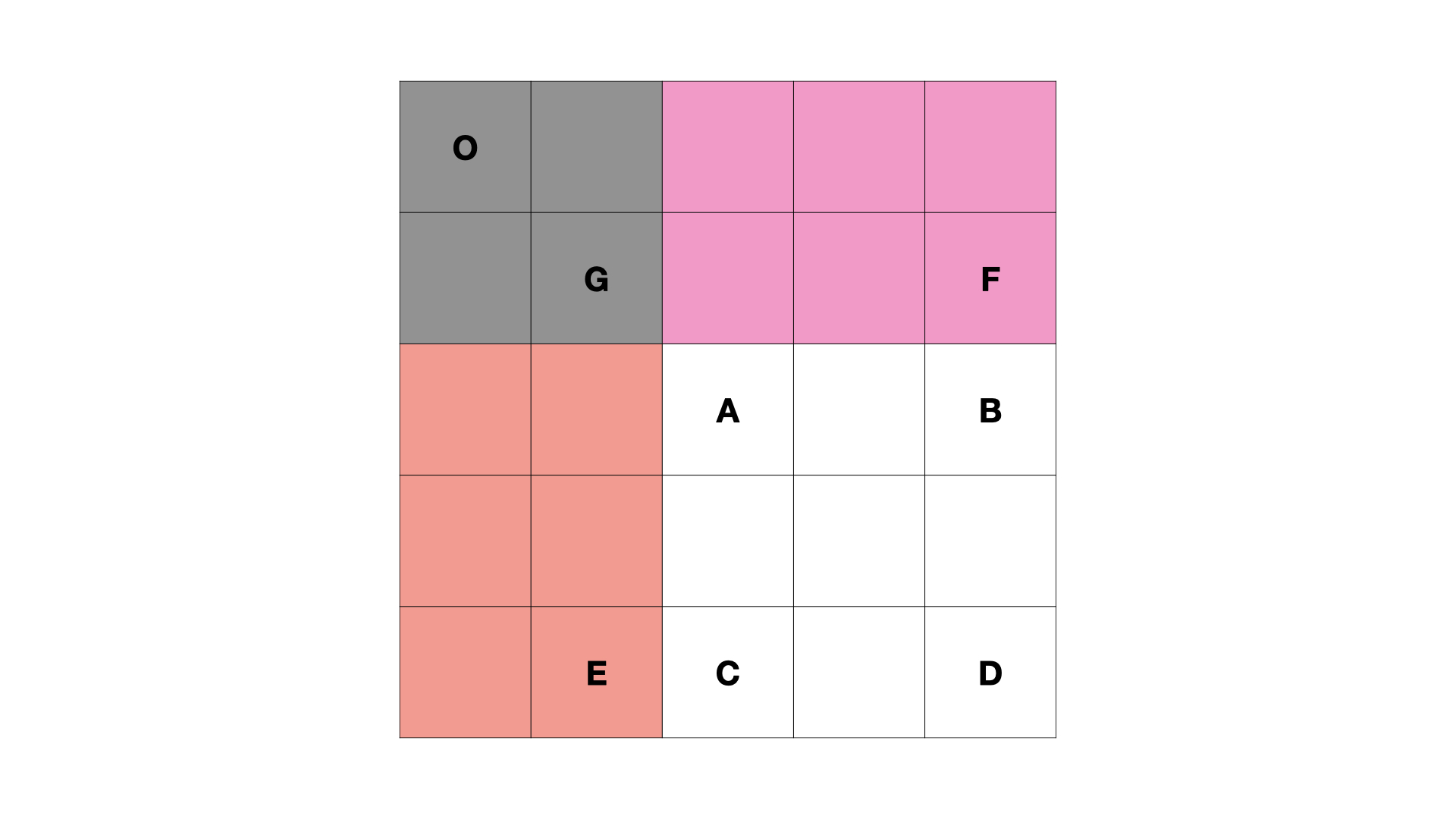
同样利用一张图来说明：

S(A, D) = S(O, D) - S(O, E) - S(O, F) + S(O, G)
304.002.jpeg

preSum[row2][col2]−preSum[row2][col1−1]−preSum[row1−1][col2]+preSum[row1−1][col1−1]

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class NumMatrix {

    int[][] preNum; 
    public NumMatrix(int[][] matrix) {
        //从[0][0]开始进行计算
            preNum = new int[matrix.length+1][matrix[0].length+1];
            if(matrix.length>0){
                for(int i=1;i<=matrix.length;i++){
                    for(int j=1;j<=matrix[0].length;j++){
                        //第一张图所示
                            preNum[i][j]=preNum[i-1][j] + preNum[i][j-1]-preNum[i-1][j-1] +matrix[i-1][j-1] ;
                    }
                }
            }
    }
    
    public int sumRegion(int row1, int col1, int row2, int col2) {
        //减去边角加上重复的部分，加上了第
            return   preNum[row2+1][col2+1] - preNum[row2+1][col1] - preNum[row1][col2+1] + preNum[row1][col1];
    }
}

和为 K 的子数组

那我把所有子数组都穷举出来，算它们的和，看看谁的和等于 k 不就行了

时间复杂度 O(N^2)

空间复杂度 O(N)

img

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
    /**
     * @description: 要求是计算出子数组和为k的值, 如果就是说利用前缀和将每个元素计算出来，
     * 利用二重循环遍历,将每个数组可能进行迭代
     * @author jwz
     * @date: 2022/3/26
     */

    public int subarraySum(int[] nums, int k) {

//        构造前缀和 ,指定数组
        int[] preNum = new int[nums.length + 1];
//        初始化数组
//  数组是从0开始，当我们进行相加时，先取出前缀和的第0个与数组的第0个,不能写等于数组是从0k开始进行遍历
        for (int i = 0; i < nums.length; i++) {
            preNum[i + 1] = preNum[i] + nums[i];
        }
        int res = 0;
//        因为从前缀数组中获取值，所以从一开始为数组的有效值
        for (int i = 1; i <= nums.length; i++) {
//            第一次循环先获取更新一个元素，再将所有的元素进行组合一遍
            for (int j = 0; j < i; j++) {
                if (preNum[i] - preNum[j] == k) {
                    res++;
                }

            }
        }
        return res;
    }

优化：

image-20220327135713349

    /**
     * pre表示前缀和，表示0-i所有下标元素的和
     * 子数组和等于k的话，就是在[0,i]找一个j看是否有
     * 即pre[i] - pre[j] == k！即找到[0,i]中有多少个j满足条件即可！
     * 所以我们把 前缀和 最为key，数量最为value存入Map中！
     * 每次遍历到当前pre，只要从map中去拿pre - k作为key的value数量值即可！
     */

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
    public int subarraySum2(int[] nums, int k) {
        int count = 0, pre = 0;
        HashMap< Integer, Integer > mp = new HashMap < > ();
        mp.put(0, 1);
//        每次更新一个值有几个和它相加等于k的，我们只需要统计相加出现的次数即可
        for (int i = 0; i < nums.length; i++) {
//            获取每个数组的和
            pre += nums[i];
//            判断是否含有相加为该值的数
            if (mp.containsKey(pre - k)) {
                count += mp.get(pre - k);
            }
            mp.put(pre, mp.getOrDefault(pre, 0) + 1);
        }
        return count;
    }